Demographic and environmental stochasticity
Introduction
Not everything is always fixed in nature - naturally there is random variation that can creep into populations and this affects their growth rates and success. These processes are referred to as stochastic processes and they can come in two flavours - demographic and environmental stochastic processes. We will be modelling these processes in today’s practical.
Demographic stochasticity
The basic idea here is that populations can vary in their growth rates based on the number of births and the number of individuals which survive to the following year. In the previous practical we modelled populations with fixed growth rates but it is very unlikely that the population would grow consistantly according to that rate every year. Factors that influence demographic stochasticity might be the chances of locating and successfully attracting a mate, arriving at a breeding location and establishing a territory, carrying the offspring to term, having a successful birthing or hatching process - the list could go on. A large proportion of the ecological modelling literature has focusssed on the effect of population sizes and stochastic processes as this has major conservation implications. In today’s practical we will be investigating the the impact of stochastistic processes on varying population sizes.
Among the most important considerations here is the concept of stability. Under what conditions is a populaion most stable - that is, predictable? A good measure of stability (or its inverse - variation) is the coefficient of variation. There are two ways ecologists can calculate the CV. The first is by dividing the standard deviation by the mean - a more traditional approach. However, dividing the mean by the standard deviation \(\left(\frac{\bar{x}}{\sigma}\right)\) can be a more intuitive measure of how the variation scales with the mean. In brief - a high stability value would have a mean that is much much greater than the variation. A standard deviation that is greater than the mean would then lower the stability value. See this article for a brief discussion on this point. We will be incorporating that into our investigations for this practical. We will also be exploring how the size of the population impacts the effect that random demographic variation has on individuals of the population.
The following app is designed to run a series of simulations (you can adjust the number of simulations in the app) for one time step for two populations of varying size. These populations grow according to the discrete exponential growth model but the model parameters (birth rate \(b\) and survivorship \(S\)) are modified by random processes. The intensity of stochastic processes is the same for both populations. The measure of stochasticity is a random value drawn from the uniform distribution between zero and one using the runif() function. This random value is then compared to the survivorship and birth rates and if the returned random value is less than the rate then the there is a successful birth or survival event. If the random value is less than the rate parameter then no result is recorded. This is done for the total number of simulations and the densities of the total number of survivors and births are plotted.
Download the demographic stochasticty app here and use this app to complete the demographic stochasticity section of the Worksheet questions below
That is a very basic introduction into how one can incorporate demographic stochasticity into population modelling. Complete the questions in the prac hand-out.
Environmental stochasticity
The second important stocastic influence which we will model is from source outside our population - from the area where the population is inhabitting. These could be attributed to annual climatic variability which alters the food availability, changes in terrain which make it more difficult to move through an area, or environmental catastrophes which have dramatic implications of immediate effect. In this next section we will be modelling fluctuations in carrying capacity using the logistic growth equation from our previous practical by applying stochastic modifications to \(K\).
This modificaction to the carrying capacity is done by drawing one value from the normal distribution (using the rnorm() function) where the mean value of the distribution is the expected carrying capacity and and the standard deviation of this normal distribution represents the intensity of the environmental variability that the community might experience. You can modify both of these parameters in the app. Should the population reach a population size of less than one the population will become extinct.
Download the environmental stochasticty app here and complete the environmental stochasticity section of the Worksheet questions.
Worksheet questions
A quick refresher about how to open the apps in RStudio
1. Navigate to the links supplied above. These will take you to a DropBox repository where the app files are easily available for you to download.
2. After arriving at the DropBox page you will see a … button in the top right area of your screen. Clicking on this will present oyu with a series of options - one of which will allow you to download the app file.
3. Download this file and save it in a logical place.
4. If your computer has R and RStudio installed then double clicking on the file should open the file in RStudio.
5. Once the file is open in RStudio a green arrow/play button will appear at the top of your app file within RStudio.
6. Clicking this green arrow/play button will initiate the app.
7. The app will automatically check whether the required packages are installed - if they are the app should run smoothly. If they are not installed then please be patient while the packages download. This download period should not take more than a few minutes at the most.
Projects!
I have mentioned elsewhere in the tutorials accompanying this website that it is best if you work within RStudio’s project environment. This allows your code to be saved automatically at very regular intervals. It also aids you in keeping your work organised. Please read up on how to use this functionality by browsing through the tutorials or reading this brief section (as well as any other similar sections within this resource).
One last point - please be sure that when you are not specifically told to modify a parameter of an app that you leave the parameter at the default value. If you forget what that value is then you can quickly exit the app and start it again and then manipulate only the required parameters in order to answer the question.
Demographic stochasticity
Question 1
Estimate the mean number and the range (end points of the distribution - do not include outlier values) of births when the model parameters are:
1. \(N_{p1}0\) = 20, \(S_{p1}\) = 0.6, \(b_{p1}\) = 0.2, \(N_{p2}0\) = 60, \(S_{p2}\) = 0.2, \(b_{p2}\) = 0.9, \(N_{sims}\) = 100 (1)
2. \(N_{p1}0\) = 20, \(S_{p1}\) = 0.6, \(b_{p1}\) = 0.2, \(N_{p2}0\) = 60, \(S_{p2}\) = 0.2, \(b_{p2}\) = 0.4, \(N_{sims}\) = 300 (1)
3. \(N_{p1}0\) = 60, \(S_{p1}\) = 0.6, \(b_{p1}\) = 0.6, \(N_{p2}0\) = 100, \(S_{p2}\) = 0.2, \(b_{p2}\) = 0.9, \(N_{sims}\) = 1000 (1)
Question 2
Assume a high number of simulations – what is the general equation for calculating the mean number of births and survivors? (2)
Question 3
How does the number of simulations affect the output of the plots? What is the reason for including this functionality? (4)
Question 4
The next question of this app requires you to understand a simple but ecologically profound statistical concept - the stability version of the coefficient of variation: \(\left(\frac{\bar{x}}{\sigma}\right)\). Using basic mathematics, calculate the mean, standard deviation and stability version of the coefficient of variation for the following two sets of numbers:
c(1, 5, 4, 7, 8, 2, 4)(3)
c(15, 8, 16, 7, 21, 6, 19)(3)
Question 5
Describe the relationship between population size and the number of simulations and the coefficients of variation for births and survivors. Give reasons for why these relationships exist (5)
Question 6
This app has hopefully helped you to grasp some of the relationships between population size and the effects of stochasticity. The number of individuals seems to have an important role to play in the viability of a population and so we can use this population size and the population parameters to calculate a series of metrics useful in determining extinction probabilities. one such equation is
\[P(extinction) = \left(\frac{d}{b}\right)^{N_0}\]
where \(d\) is the death rate (\(1 - S\)) and \(b\) is the birth rate. Using this equation show that population size is an important contributer towards determining the probability of extinction under conditions where the birth rate is greater than the death rate and the death rate is greater than the birth rate (6)
Environmental stochasticity
Question 1
Consider the difference between discrete and continuous population modelling techniques. Which technique has likely been used in this example? Give mathematical and ecological reasons for your answer (5)
Question 2
Provide the equation that could be used to develop this kind of figure. List the variables used together with a short description of each variable’s purpose in the equation (6)
Question 3
Set the population parameters to \(N_0\) = 50, \(K\) = 100, \(r\) = 0.4, \(years\) = 100. How does changing the intensity of environmental variability affect the time until the population goes extinct? (3)
Coding questions
Idea behind the demographic stochasticity model
Building a model to depict stochasticity is slightly more complicated than our previous examples. Whilst there are some parameters the you will likely be used to from the previous practical there is a new parameter which is called “sims”. This is simply the number of times we are going to gather simulated data from our populations in order to plot distributions describing the births and deaths - you’ll see where we are going in a few more steps.
For this model we will be exploring how random demographic variation affects populations of two different sizes. We are interested in understanding how random fluctuations in birth rates and survival rates affects the viability of a population. To do this we will need to define a few vectors in which we will store the number of births and survivors that our population has. Each position within the vector will contain the total births and deaths for each simulation applied to each population. We have two sets of vectors, one for each population.
Now comes the cool part! We will use a similar principle to what we did in our last prac by employing a for loop to carry out the population size calculations for each time period which will then be used to populate our vectors. We will actually be using three for loops. The first loop (which we will call the global for loop) will step through each of the simulations - from 0 through to sims. Within the global loop we define four more variables - these are where we will store the counts of the number of individuals which survive and give birth for each of the two populations we are dealing with. These variables are reset to zero at the beginning of each new simulation. Following on from this are two independent for loops - one for each population. These loops step through each individual of their respective populations to count the number of individuals which survive and give birth. It is at this point where we incorporate stochasticity - if a randomly generated number is less than the populations’ survival and birth rate parameters then the individual in question survives or gives birth. And then at the end of these two for loops we assign our collected counts to our vectors which we created outside of our loops at the position corresponding to the simulation that has just been run.
After this we will have collected all the data we will need. We can then combine our data into a dataframe for plotting. We will bind population one data and population two data into two separate data frames (using cbind to bind columns and as.data.frame to turn those columns into a data frame) and then combine those two data frames into one final data frame using bind_rows.
Question 1
An important method for working with dataframes is data wrangling. This practical introduces this idea in practice.
1. Describe what “data wrangling” is (3)
2. In R data wrangling is usually carried out using the spread() and gather() functions from the tidyr package. With reference to the package’s and functions’ websites but in your own words, describe how these two functions work to manipulate or wrangle dataframes. You may include your own examples (not those from the websites) if you wish (6)
Question 2
The ggplot2 package has some very impressive functionality which allows for unique and professional quality plots which display large amounts of information. One interesting way that one can include more information on a plot is through facetting. Explain what facetting is and how to use it in ggplot2. Also describe how the facet labels can be changed from what is in the dataframe using the labeller argument (4)
Question 3
The followoing code is supposed to produce an utput to model demographic stochasticity, however, there are four problems with the code that are affecting the faceting - two are with the construction of the dataframe and two are concerned with the formatting of the actual plot. Edit the following code to match the figure below (this figure has been modified from the one in the Shiny App - the CV calculations have been removed) and copy it into your Word document together with your completed figure output. Be sure to include comments on what you have changed and brief reasons why you have done so (8)
library(tidyr)
library(dplyr)
library(ggplot2)
library(viridis)
sims <- 100 ## number of simulations to run
pop1 <- 10 ## population 1 size
survive1 <- 0.6 ## population 1 survival probability
birth1 <- 0.4 ## population 1 birth probability
pop2 <- 200 ## population 2 size
survive2 <- 0.5 ## population 2 survival probability
birth2 <- 0.6 ## population 1 birth probability
Trial = seq(from = 0, to = sims, by = 1)
Survivors1 = numeric(length = sims + 1)
Births1 = numeric(length = sims + 1)
Survivors2 = numeric(length = sims + 1)
Births2 = numeric(length = sims + 1)
for (i in 0:sims) {
survive_count1 <- 0
birth_count1 <- 0
survive_count2 <- 0
birth_count2 <- 0
for (j in 0:pop1) {
ifelse(runif(1) < survive1,
survive_count1 <- survive_count1 + 1,
survive_count1 <- survive_count1)
ifelse(runif(1) < birth1,
birth_count1 <- birth_count1 + 1,
birth_count1 <- birth_count1)
}
for (k in 0:pop2) {
ifelse(runif(1) < survive2,
survive_count2 <- survive_count2 + 1,
survive_count2 <- survive_count2)
ifelse(runif(1) < birth2,
birth_count2 <- birth_count2 + 1,
birth_count2 <- birth_count2)
}
Survivors1[i] <- survive_count1
Births1[i] <- birth_count1
Survivors2[i] <- survive_count2
Births2[i] <- birth_count2
}
survive_birth_df1 <- as.data.frame(cbind(Trial,
Survivors = Survivors1,
Births = Births1))
N10 <- gather(survive_birth_df1,
key = "Aspect",
value = "Value")
survive_birth_df2 <- as.data.frame(cbind(Trial,
Survivors = Survivors2,
Births = Births2))
N100 <- gather(survive_birth_df2,
key = "Aspect",
value = "Value")
survive_birth_df <- bind_rows(N10, N100, .id = "Population")
ggplot(survive_birth_df) +
geom_density(aes(x = Value,
colour = Aspect,
fill = Aspect),
alpha = 0.4) +
facet_wrap(~ Aspect,
scales = "free_x",
labeller = as_labeller(c("1" = "Population 1",
"2" = "Population 2"))) +
labs(x = "Population size",
y = "Density",
colour = "Population \nparameter",
fill = "Population \nparameter") +
theme(panel.background = element_rect(colour = "black",
fill = "white"),
panel.grid = element_blank(),
axis.title = element_text(colour = "black",
size = 14),
axis.text = element_text(colour = "black",
size = 12),
legend.text = element_text(colour = "black",
size = 12),
legend.title = element_text(colour = "black",
size = 14)) +
scale_color_viridis(discrete = TRUE, end = 0.8) +
scale_fill_viridis(discrete = TRUE, end = 0.8)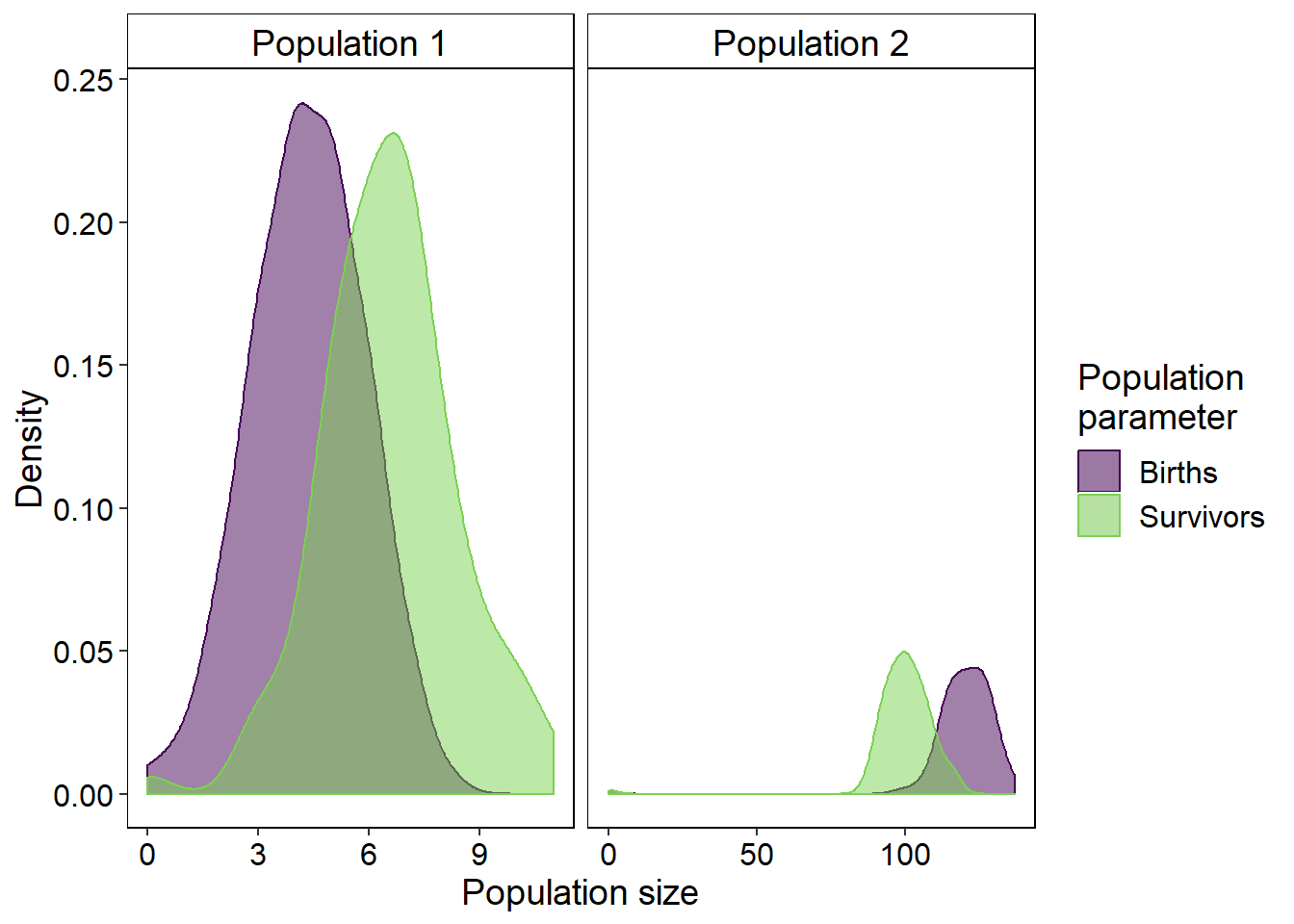
- For this second coding question there are six errors (three logical and three cosmetic) which are preventing the code from running. Identify and correct these errors in the following code. Present your corrected code and figure output together with a description and your proposed solution for each of these errors in a Word document (12)
library(ggplot2)
nyears <- seq(from = 1, to = 20, by = 1)
N <- c(50, rep(0, times = 20 - 1)) # Create an open vector for data
r <- 0.5
K <- 100
en_var <- 0.2
for (i in 1:length(nyears)+1) {
## carrying capacity variability
randK <- rnorm(n = 1, mean = K, sd = en_var*K)
ifelse(N[i - 1] <= 1,
N[i] <- 0,
N[i] <- (r*N[i - 1]*(1 - (N[i - 1]/randK))))
ifelse(N[i] > 0,
N[i] <- 0,
N[i] <- N[i])
}
log_stoch <- as.data.frame(cbind(nyears, N))
ggplot(log_stoch) + geom_point(aes(x = nyears, y = N)) +
geom_hline(yintercept = 0) +
geom_line(aes(x = nyears, y = N)) +
theme(axis.title = element_text(colour = "black",
size = 14),
axis.text = element_text(colour = "black",
size = 12))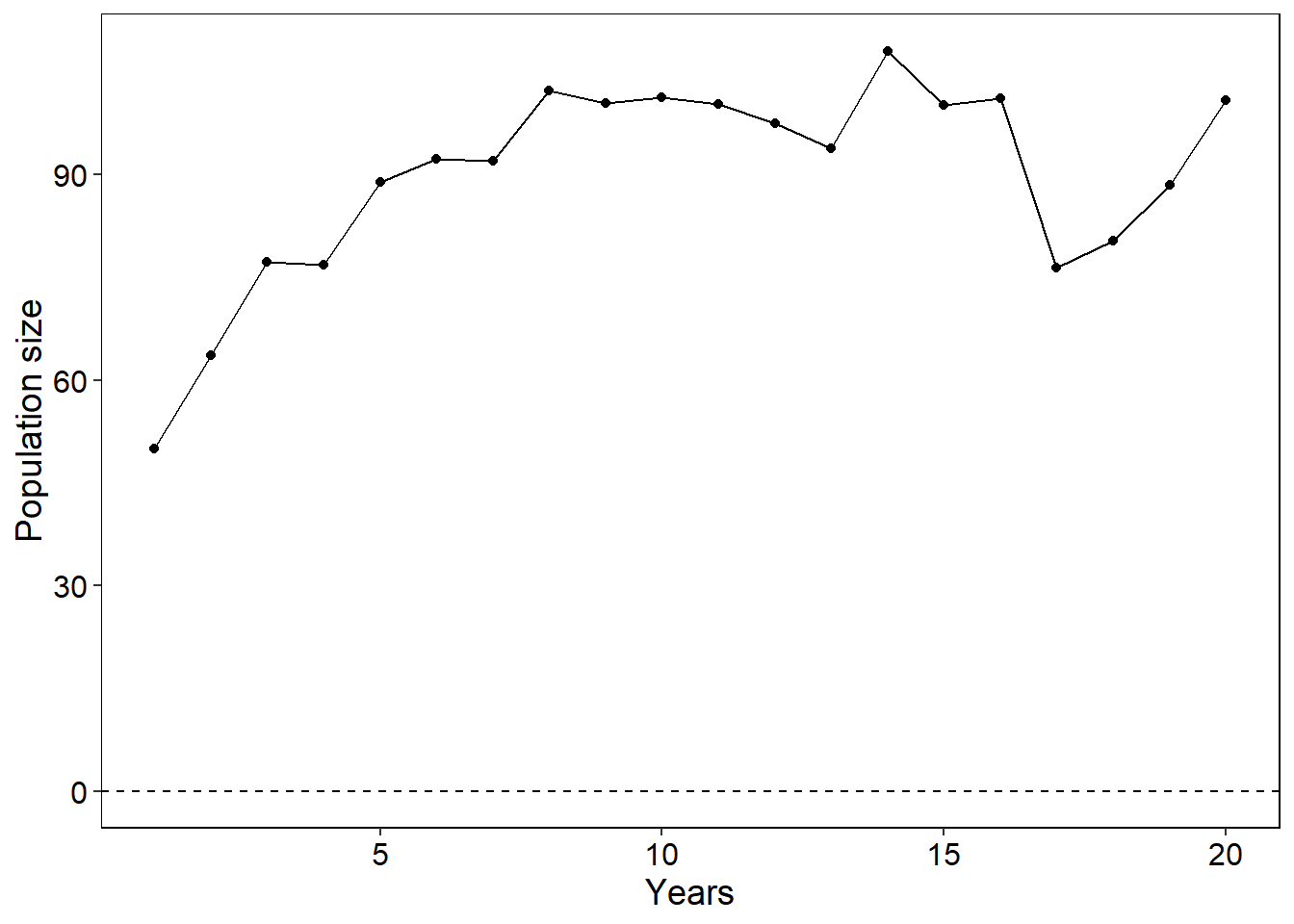
Application questions
Demographic stochasticity
Question 1
Almost every population on earth is affected by demographic stability. List and briefly explain five sources of demographic stochasticity (10)
Question 2
Small populations are an important topic in conservation biology. Comment on the importance of population size in conservation. Make refernece to at least three scientific papers (8)
Environmental stochasticity
Question 1
Consider the environmental stochasticity model. Commment on how one other type of environmental modifiers could be incorporated into our environmental stochasticity model (4)
Question 2
There is substantial variation in climate and resource availability across biomes. Some biomes are more stable (less stochastic events occur) than other biomes. Within those biomes there is also variability of species resillience to environmental variability. Below is a table which contains three biomes and two species which live in each of the biomes. One species is very resilient and the other is not. Using your knowledge on the properties of common biomes and the species that live in these biomes, order the biomes from most to least stable and identify which species is the resillient one and which species is the sensitive one for each of the biomes. Give reasons (at least two) for each aspect of your answer (21)
| Habitat | Animal |
|---|---|
| Savanna | Kudu |
| Zebra | |
| Rainforest | Tenrec |
| Tree frog | |
| Desert | Camel |
| Mouse |
Combined stochasticity
- In this practical we have considered demographic and environmental stochasiticity in isolation, however, in real world conservation scenarios these two aspects often need to be considered together. This is often done using a method called population viability analysis (PVA). In South Africa one of the most important conservation efforts has been that of the African elephant. By making reference to this article (you will be able to download it when connected to the university LAN, through JSTOR or Google Scholar) define what population viability analysis is and identify both demographic and environmental stochasticity examples that the authors incorporated into their modelling (10)