Common resource competition
Introduction
In the logistic model of population growth we saw that resource limitation can be included in an abstract way by incorporating some kind of carrying capacity for a population. But, what if there are also other species competing for the same resources? Depending on the strength of competition, competing species can reduce equilibrium population abundance to below the carrying capacity. To jog your memory, here is the discrete-time version of logistic growth:
\[ N_{t+1} = N_{t} + rN_{t}\left(1-\frac{N_{t}}{K}\right) \]
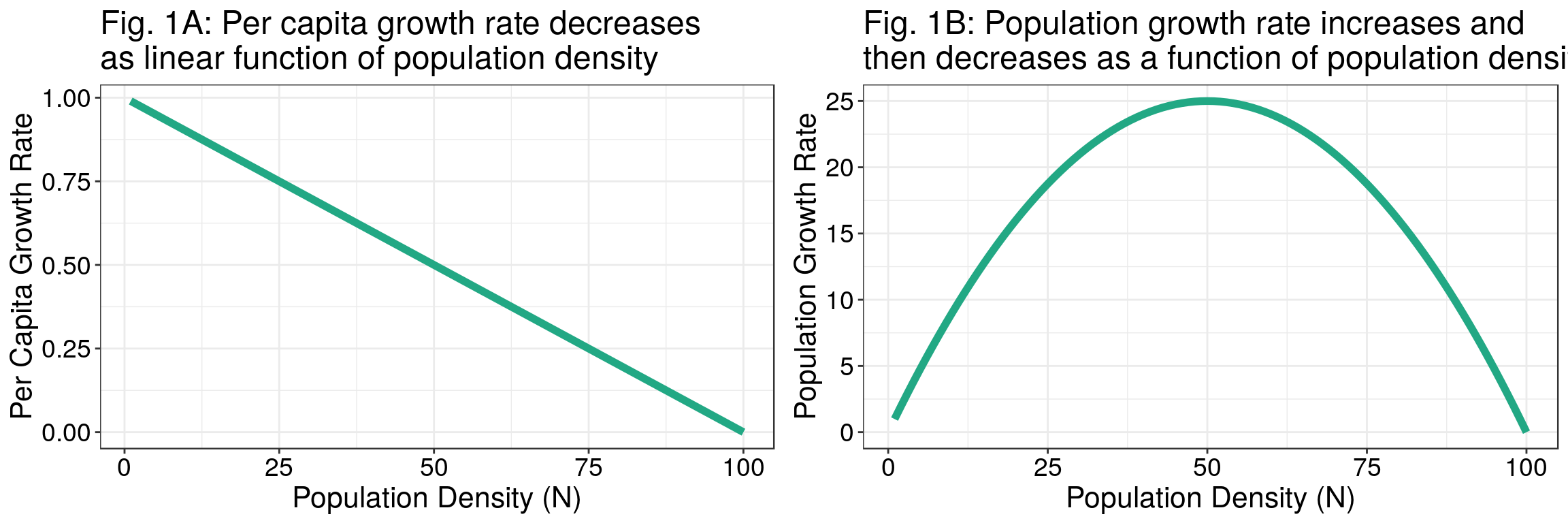
where \(r\) is the intrinsic per capita growth rate, \(N\) is the population abundance, and \(K\) is the carrying capacity. The \(\left(\frac{N}{K}\right)\) term represents the intraspecific competition (density-dependence) – the closer \(N\) comes to \(K\), the slower the population grows. However, carrying capacity is a notoriously difficult term to define and quantify. Peter Chesson (2000) describes a more intuitive way to think about population growth by assuming that “per capita growth rates are linear decreasing functions of the density” of the population (Figure 1A). When this is the case, population growth rate starts low when a species is at low abundance (low \(N\), high \(r\)), increases to a maximum when a species reaches a moderate abundance (medium \(N\), medium \(r\)), and then decreases as the population reaches a high density (high \(N\), low \(r\)) (Figure 1B).
Looking at the model from an interspecific competition perspective allows us to rewrite the logistic growth equation as:
\[ N_{t+1} = N_{t} + rN_{t} \left(1-\alpha N \right) \] where \(\alpha\) is the absolute effect of intraspecific competition, and is equal to \(1/K\) from the previous equation. If \(\alpha\) is very small, then intraspecific competition (density-dependence) is negligible. If \(\alpha\) is very large, then intraspecific competition strongly limits population growth and size. The reason we go into all this trouble to rewrite the logistic growth equation is to make it easier to include the possible effects of other species on population growth. But first, let’s make the equation a little more simple by writing it in terms of population growth rates \(\left(\frac{dN}{dt} \right)\), rather than population size, and by adding subscripts to denote we are talking about Species \(i\):
\[ \frac{dN_i}{dt} = rN_{i} \left(1-\alpha_{ii} N_i \right) \]
Notice how we have now dropped the \(t\) subscripts because we are now defining population growth at any instantaneous point in time. Also notice that we added two \(i\) subscripts to \(\alpha\). Here \(\alpha_{ii}\) reads as the effect of Species \(i\) on Species \(i\). To include the effect of another species, we assume that growth is further limited by a simple function of the number of the other species; \(\alpha_{ij}N_j\), where \(\alpha_{ij}\) reads as: “the effect of Species \(j\) on Species \(i\)”. Putting it all together, we can write equations for a two-species community as:
\[ \begin{align} \frac{dN_1}{dt} &= r_1 N_1 \left(1- \alpha_{11} N_1 - \alpha_{12} N_2 \right) \\ \frac{dN_2}{dt} &= r_2 N_2 \left(1 - \alpha_{22} N_2 - \alpha_{21} N_1 \right) \end{align} \]
where the new parameter \(\alpha_{21}\) is the absolute interspecific competition coefficient describing the effect of Species 2 (\(N_2\)) on Species 1 (\(N_1\)). Recall that the fundamental requirement for species coexistence is that each species must be able to increase from low density (i.e., when it is rare in the community), implying that intraspecific competition must be greater than interspecific competition. Put more simply, each species must limit individuals of its own species more than it limits individuals of other species.
Because the \(\alpha\)’s control intra- and interspecific competition in the Lotka-Volterra model, we can state the criterion for coexistence of both species mathematically as:
\[ \alpha_{jj} > \alpha_{ij} \]
meaning that Species \(j\) for instance cannot competitively exclude Species \(i\) if the effect Species \(j\) has on itself is greater than the effect it has on Species \(i\). For a two species community, the coexistence is stable if, and only if:
\[ \alpha_{11} > \alpha_{21} \quad \text{AND} \quad \alpha_{22} > \alpha_{12}. \]
The multispecies equation
Just in case you ever see this in a paper, it is often written in the multispecies case as:
\[ \frac{dN_{i}}{dt} = r_{i}N_{i} \left(1 - \alpha_{ii} N_{i} - \sum_{i \neq j}^S \alpha_{ij}N_{j}\right) \]
where Species \(i\) is the species of interest and \(S\) is the number of species in the community.
Incorporating carrying capacity
By now you should understand that carrying capacity plays a pretty important role in defining how much and how quickly populations can grow. In the previous examples we incorporated carrying capacity into the model by accounting for the effect of Species 1 on Species 1 and Species 2 on Species 2. But there are other methods which can be more appropriate depending on data availability. Suppose we have two Species (\(N_1\) and \(N_2\)) utilising one shared set of finite resources (\(K\)). It is likely that the set of finite resources cannot sustain both Species 1 and Species 2 at their respective carrying capacities - one species would likely require more resources than the other species and so we would have two carrying capacities (\(K_1\) and \(K_2\)) and two different population growth rates (\(r_1\) and \(r_2\)). From this we can develop two equations to model the two species’ population sizes through time:
\[ \begin{align} N_{1,t+1} = N_{1,t} + r_1N_{1,t}\frac{K_1-N_{1,t}}{K_1} \\ \\ N_{2,t+1} = N_{2,t} + r_1N_{2,t}\frac{K_2-N_{2,t}}{K_2} \end{align} \]
This is a step in the right direction – by incorporating carrying capacity into our equations we have successfully accounted for the effect that conspecifics (individuals of the same species) have on each other but we have not accounted for the interspecific competitive effects (i.e. increases in Species 2’s population on the growth rate of Species 1). As the growth rate is dependent on the resources available to the population in question, a good place to incorporate this competitive effect would be around \(K_1-N_{1,t}\) term. We could simply minus \(N_{2,t}\) as well but it is also likely that the two species do not have exactly the same effect on the available resources. Thus we can incorporate the competition coefficient modifier at the \(N_{2,t}\) term and so the numerator would then be \(K_1-N_{1,t} - a_{12}N_{2,t}\).
Often ecologists are interested in whether one species will out compete another or whether these two species will be able to coexist and persist at stable equlibria. To investigate this we can consider scenarios when there will be no change in the population size from time \(t\) to time \(t+1\). That is \(N_{1,t+1}\) equals \(N_{1,t}\). This can be true for a number of scenarios such as when \(r = 0\) or when \(N_{1,t} = 0\). Those are rather simple scenarios but there will also be no change in the population when \(K_1-N_{1,t} - a_{12}N_{2,t} = 0\). We can easily convert this equation to a linear equations of the form \(y = a + bx\) – the equation for a straight line. This line can then represent situations where Species 1 will not grow and so we call it the “zero net growth isocline” (ZNGI). We can do a similar thing for Species 2. When these lines are plotted on a Cartesian plane the lines can provide us with important information. Let’s focus on the axes intercepts for a moment. When \(N_{1,t} = 0\) we have a situation where \(K_1 = a_{12}N_{2,t}\) which translates to \(N_{2,t} = \frac{K_1}{a_{12}}\). Similarly, if \(N_{2,t} = 0\) then \(N_{1,t} = K_1\). These equations state that if there are \(\frac{K_1}{a_{12}}\) individuals of species 2 then there will be no resources for Species 1 and so Species 1 will be excluded. Similarly, if there are no individuals of Species 2 then Species 1 will reach its carrying capacity.
The best way to understand this is by visualising the model outputs together with the ZNGI curves for the two species. The first figure below shows the model outputs and the second figure contains the ZNGI curves. The top figure is fairly intuitive to interpret – Species 2 is excluding Species 1. The second figure is slightly trickier but helps us better visualise the dynamics between these two species. The axes of a ZNGI curve represent the population sizes of two species. In this example both species start at a population size close to zero. They then grow roughly at the same rate but then the curve begins to bend backwards towards the top of the y-axis. Based on the straight line equations that represent these ZNGI curves we can quickly work out what is going on here. They dotted line’s y-intercept represents \(K_2\) = 1300 and the solid line’s x-intercept represents \(K_1\) = 800. Because \(\alpha_{12}\) is greater than \(\alpha_{21}\), Species 2 is a more competitive species than Species 1 and so Species 2 excludes Species 1.
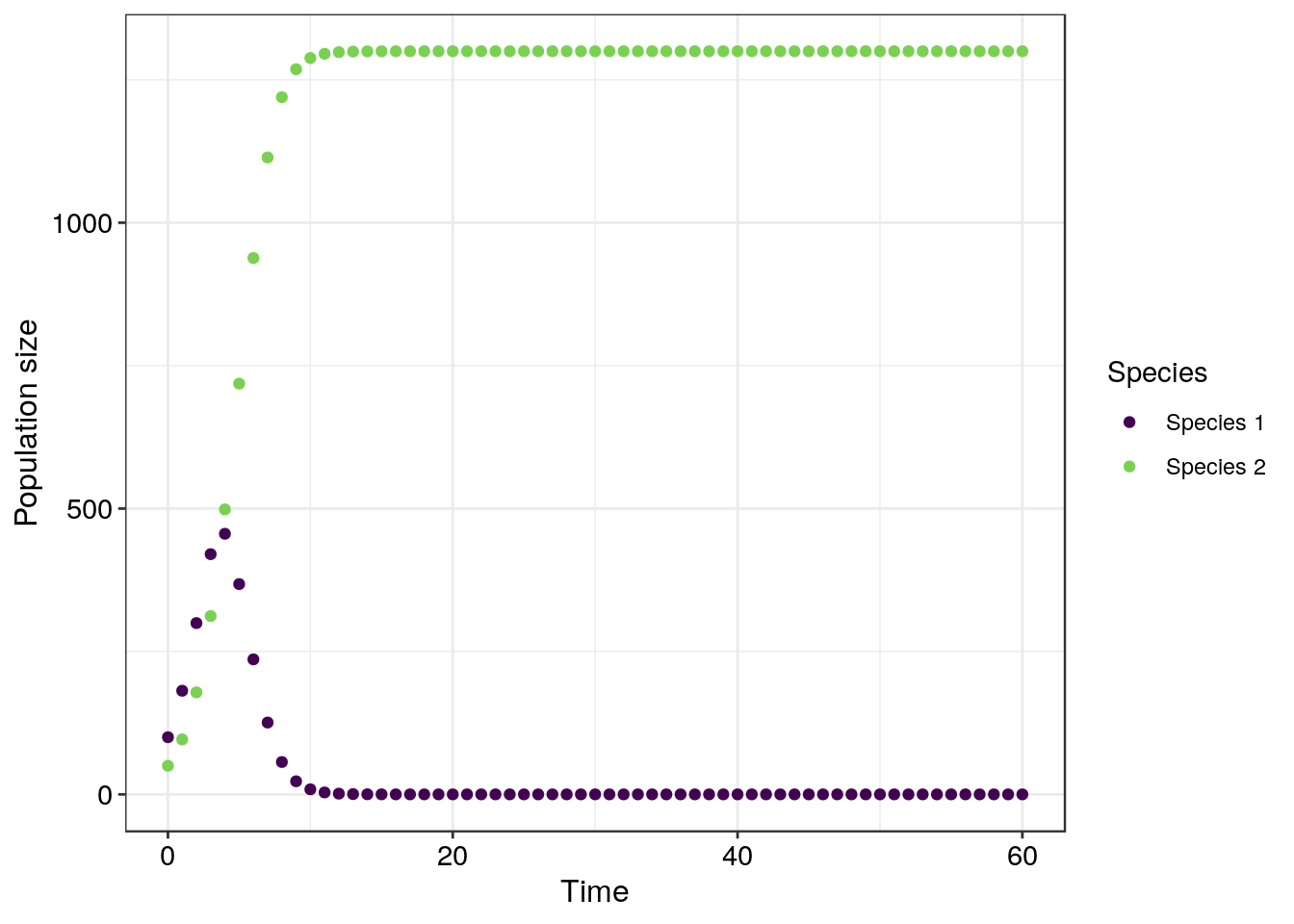
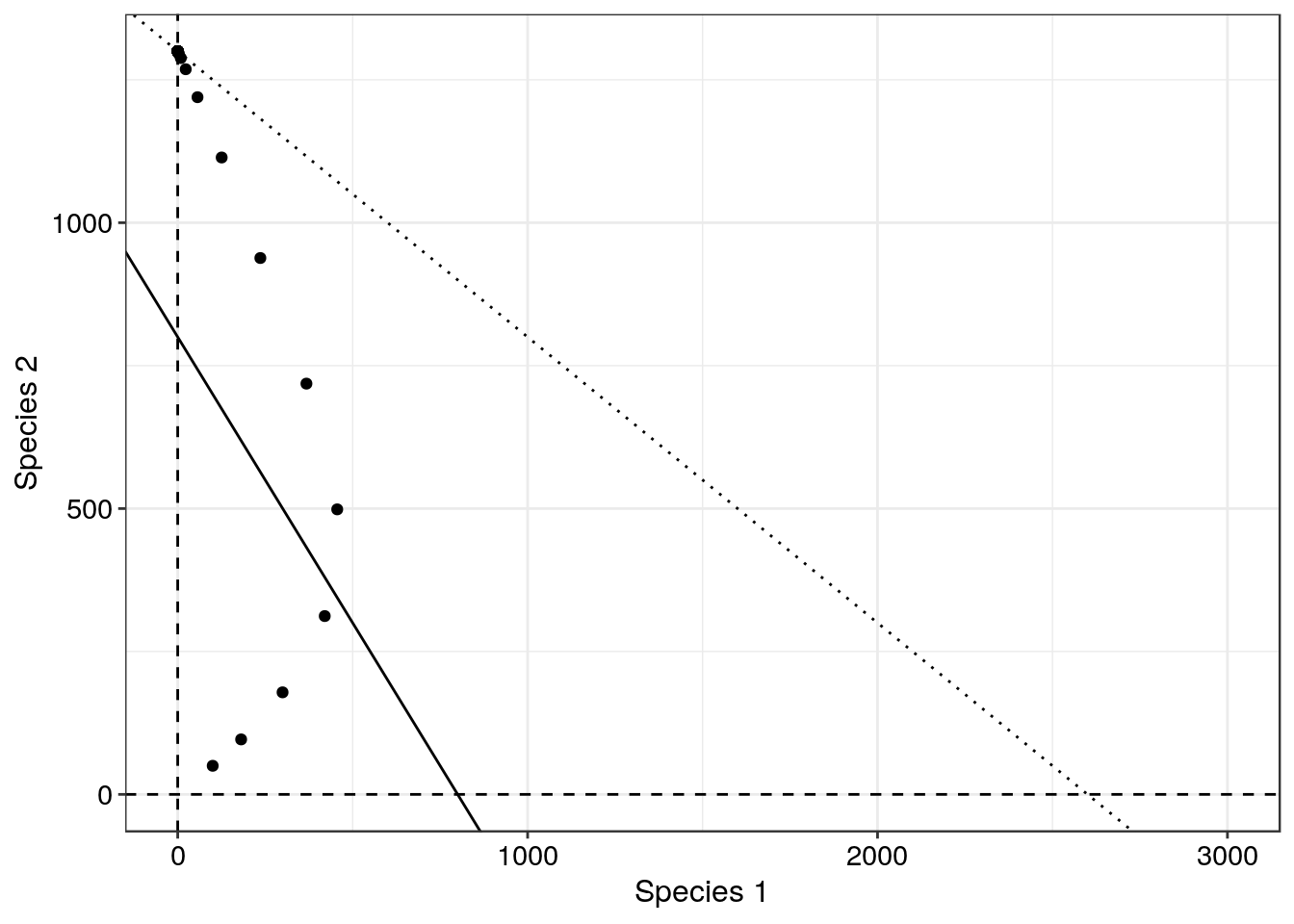
Table of parameters and states
To keep everything clear, here is a table of model states and parameters.
| Parameter | Definition |
|---|---|
| \(N_{i}\) | The abundance (or biomass, depending on units) of Species \(i\) |
| \(r_{i}\) | Species \(i\)’s intrinsic per capita growth rate |
| \(K_{i}\) | Population carrying capacity derrived from the resources available to Species \(i\) |
| \(\alpha_{ij}\) | Interspecific competition coefficient (effect of Species \(j\) on Species \(i\)) |
Parameter exploration
Download the common resource competition ZNGI app here and answer the Worksheet questions below.
Worksheet questions
Common resource competition (30)
Use only Figure 1 of the app to answer the following questions
Question 1
Under what conditions will one species exclude the other (4)
Question 2
Under what conditions will both species coexist (5)
Question 3
Use both Figure 1 and Figure 2 from the app to answer the following questions
Reload the app and set the competition coefficient parameters to \(K_1\) = 850, \(K_2\) = 1500, \(\alpha_{ij}\) = 0.7, \(\alpha_{ji}\) = 1.3 and answer the following questions:
- What does it mean that \(\alpha_{ij}\) = 0.7 and what kind of competition (interspecific or intraspecific) is the target species impacted by (2)
- What does it mean that \(\alpha_{ji}\) = 1.3 and what kind of competition (interspecific or intraspecific) is the target species impacted by (2)
- Describe the output of Figure 2. Be sure to describe the ZNGI curves and the population’s growth trajectory in full (5)
Question 4
Describe in detail what the components of the second plot represents and give suggestions for why this kind of plot is useful (4)
Question 5
- Describe the difference between stable and unstable equlibria (2)
- State under what conditions one might find
- stable competitive exclusion (2)
- stable coexistence (2)
- unstable competitive exclusion (2)
- stable competitive exclusion (2)
Question 6
Are there a set of parameters where both species in this model will become extinct? Explain your answer (2)
Coding questions (15)
Based on the coding challenges you have been exposed to previously you should be able to produce the changes in population sizes through time. This week’s coding challenge will require you to generate the data required to plot the ZNGI curves and the population sizes. Correct the following code to produced a figure that resembles the one below. You will need to construct the plot yourself. Useful functions for you to read up on will be geom_abline() and geom_hline() and geom_vline().
list.of.packages <- c("ggplot2")
#checking missing packages from list
new.packages <- list.of.packages[!(list.of.packages %in% installed.packages()[,"Package"])]
#install missing ones
if(length(new.packages)) install.packages(new.packages, dependencies = TRUE)
library(ggplot2)
# define population parameters
N01 <- 5
N02 <- 5
K1 <- 500
K2 <- 400
r1 <- 1
r2 <- 1
a12 <- 0.9
a21 <- 1.5
time <- seq(from = 0, to = 60, by = 1)
# define lengths of population vectors and initial values
N1 <- c(N01, rep(0, length(time)-1))
N2 <- c(N02, rep(0, length(time)-1))
# populate the two population vectors
for (i in 2:length(time)) {
# insert the two formulae for calculating the population sizes at each time step here
}
df1 <- as.data.frame(cbind(time, N1, N2)) # combine these three vectors into on data frame called df1
colnames(df1) <- c("Time", "Species 1", "Species 2") # rename the columns of df1 to the values on the right
# plot the output of the data and the ZNGI curves here using ggplot2()
Application questions (48)
The models used in this practical have several key assumptions. Identify and discuss these assumptions with reference to the model parameters and provide suggestions on how these assumptions can be improved upon (6)
When species compete with other species there are several outcomes that can occur. Briefly explain and give two ecological examples with reference to scientific publications of facilitation, exclusion, and co-occurrence in relation to competition interactions (9)
The central aspect of either of the two competition equations used in this practical are the competition coefficients. Discuss how these values could be estimated using field methods – 1 mark per method (5)
Conservationists and ecologists often need to employ these (or very similar) equations when managing conservation areas. Another application of these methods is when predicting the effects of new species introductions on species currently inhabiting a given area. In the form of a one page essay citing at least eight difference scientific publications, discuss the real world applications of these competition type population models to invasive species introductions and control/management and conservation reserves where several species depend on a common resource which could result in competitive exclusion or facilitation.
- Structure your essay around at least eight well explained points with preferably a unique reference (or more than one reference) for each point. Consider keeping to the rule of “one idea, one paragraph” (16)
- Marks will also be awarded for
- logical structure and argument flow (4)
- spelling and grammar (4)
- and referencing correctness (4)
- Total marks (28)